After series of 11 blogs posts about Conflict-free Replicated Data Types, it's time to wrap up. This time let's discuss various optimizations that could be applied to CRDTs working at higher scale.

Other blog posts from this series:

Since we're talking about optimizations for structures and protocols we already described in the past, a prerequisite here is to have an understanding of things like convergent maps/documents, principles of delta- and operation-based protocols and good understanding of vector clocks. Preferably you also want to have some general knowledge of durable data stores (like B+Trees and LSM trees) and database indexes.

Larger than memory CRDTs

Let's start with optimization that it's not really CRDT specific. All data structures we covered so far, had simple in-memory representations. Making them persistent sounds easy - just serialize/deserialize them on demand - but the problems starts when this process is expected to be efficient and working for high volumes of data.

When we're talking about a huge structures - the ones that could potentially not fit into memory - it's kind of obvious that we're need a way to store them in segments that are easy to navigate on disk. Most of the on-disk structures, like B+Trees or LSM trees, are exposed to users in form of a simple transactional, ordered key-value store. These key-value pairs are atoms used for data navigation: you set cursor position by seeking for a given key (or prefix of a key) and then are free to move forward over all entries with keys lexically higher than current cursor pointer, usually at pretty low cost since they involve sequential disk reads. Usually these entries are read as whole - no matter what is the size of value stored in a given entry, since its most atomic location unit exposed by the data store, it will be read as whole.

Issue of state growing beyond memory capacity was a common concern for many mature higher level database offerings using key-value data stores underneath. Solution for the problem is to split a logical data type (like SQL row, sets or even whole documents) onto multiple key-value pairs.

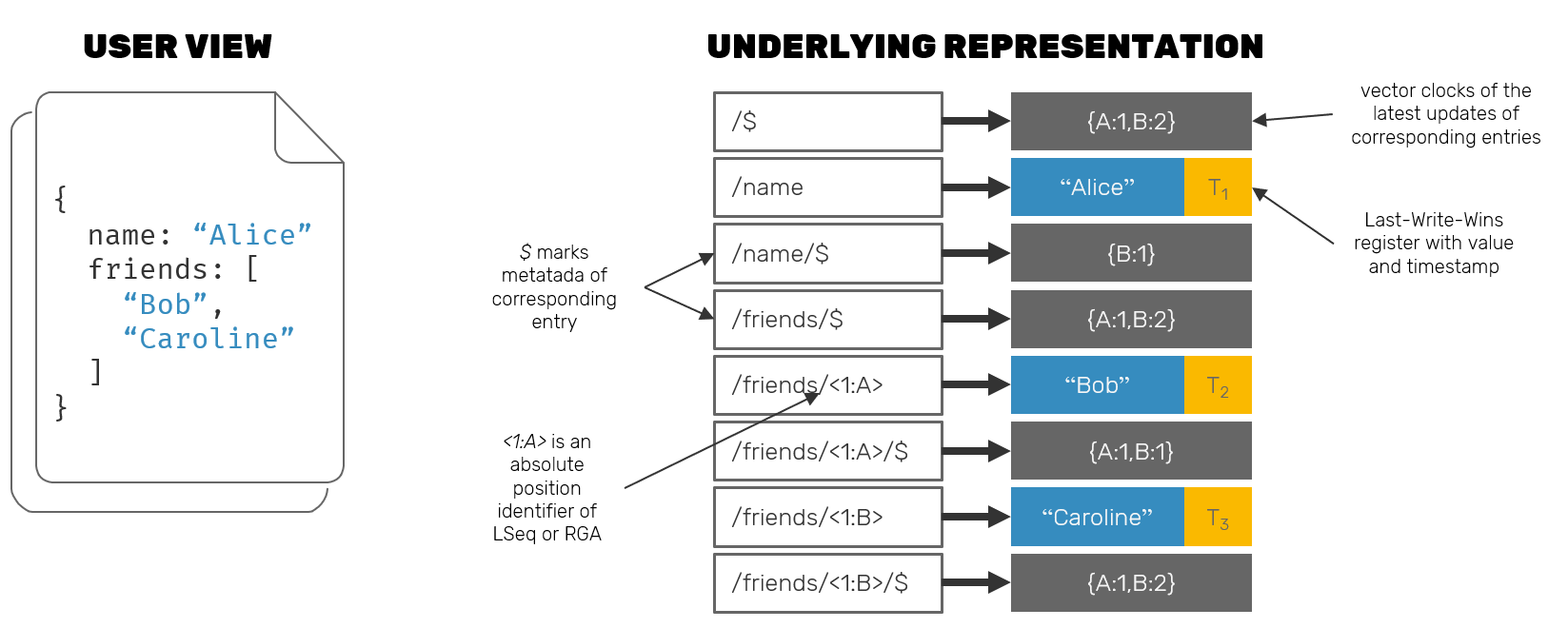
document-to-key-value-store-1

But won't this approach backfire in situation, when we'd like to return a document composed of many fields? Keep in mind that while random disk seeks may be moderately expensive, it's not the case here. As document's fields are laid out in order, reaching out for them is just a matter of doing sequential reads from disk, which are much faster. Additional advantage is that while at the API level, we're iterating the cursor over key-value entries, at the "physical" layer neighboring entries are read together from disk in pages - which can vary in size, but usually match the allocation units (4-8kB is pretty much the norm) for an underlying hardware to make writes atomic - furthermore reducing the cost of this approach.

Another question to answer is: if each key consists of the entire path in the document, starting from the root, won't this mean, that eventually the disk representation of the document will consists mainly from the keys alone? It could be true, but in practice many of the disk storage engines are prepared for this use case and use a technique called key prefix compression:

key-prefix-compression

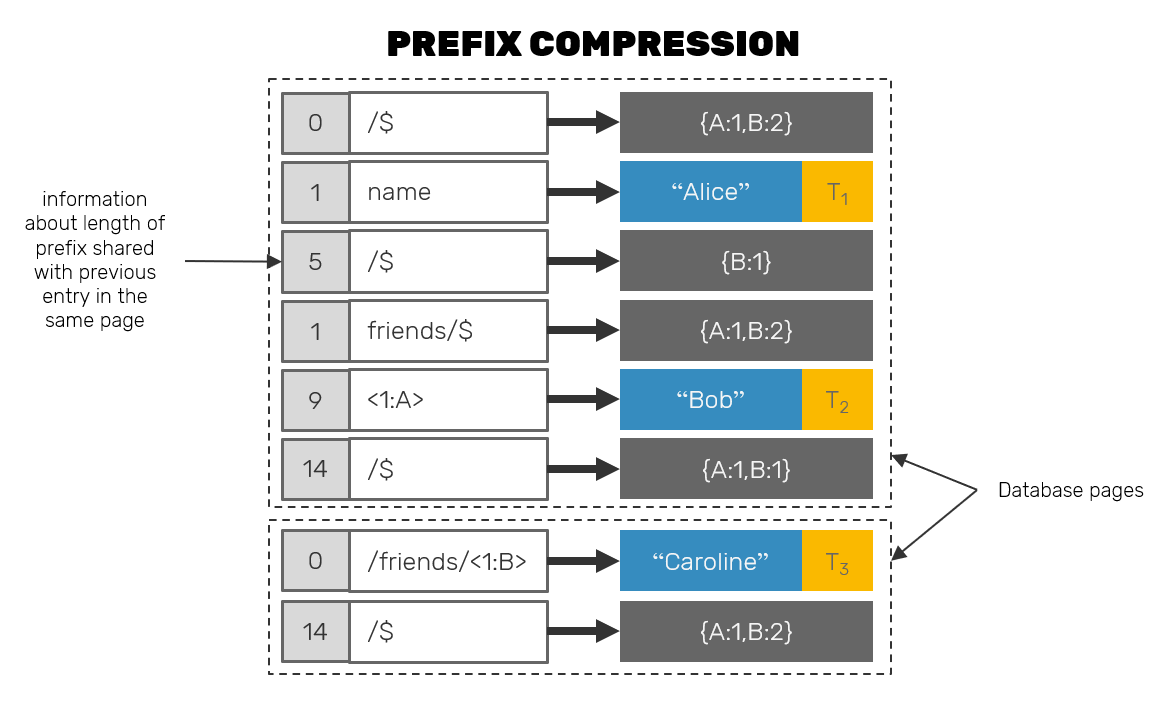
As we mentioned, entries are written and read from the disk in blocks. Now, before an entry key is stored, the engine itself checks how many bytes are shared between that key and a key of preceding entry within the same block. Then it stores that number as a prefix of the key itself, while only writing down the differentiating part of the key. Example: if entry (romulus => A) is about to be stored in a block right after entry (rome => B), we could as well write it as ([3]ulus => A) where [3] is a number of shared bytes with key of its predecessor.

Split-wise Replicated Growable Array

Back in the past we talked about optimizing indexed sequences using block-wise (or split-wise) RGA algorithm. As collaborative text editing is one of the most common places where such structure could take a place, it's important to make it as fast and responsive as possible.

You've might noticed that our PoC was far from perfect in that sense - we simply stored blocks of inserted text as arrays, which we had to split when user wanted to insert new block in the middle of old one, and we also reconstructed the whole buffer every time we wanted to present a view of our array to the user. All of this could become expensive. Can we mitigate that? It turns out we can.

If you take a closer look at the implementation details of block-wise RGA algorithms, you may notice that CRDT specifics usually depend on the metadata alone - we are usually only interested in the lenght of the content rather than content itself. In reality we could abstract it into a separate structure optimized for text manipulations (like Rope or string buffers of specific editors), while RGA-specific metadata only holds ranges that given block is responsible for.

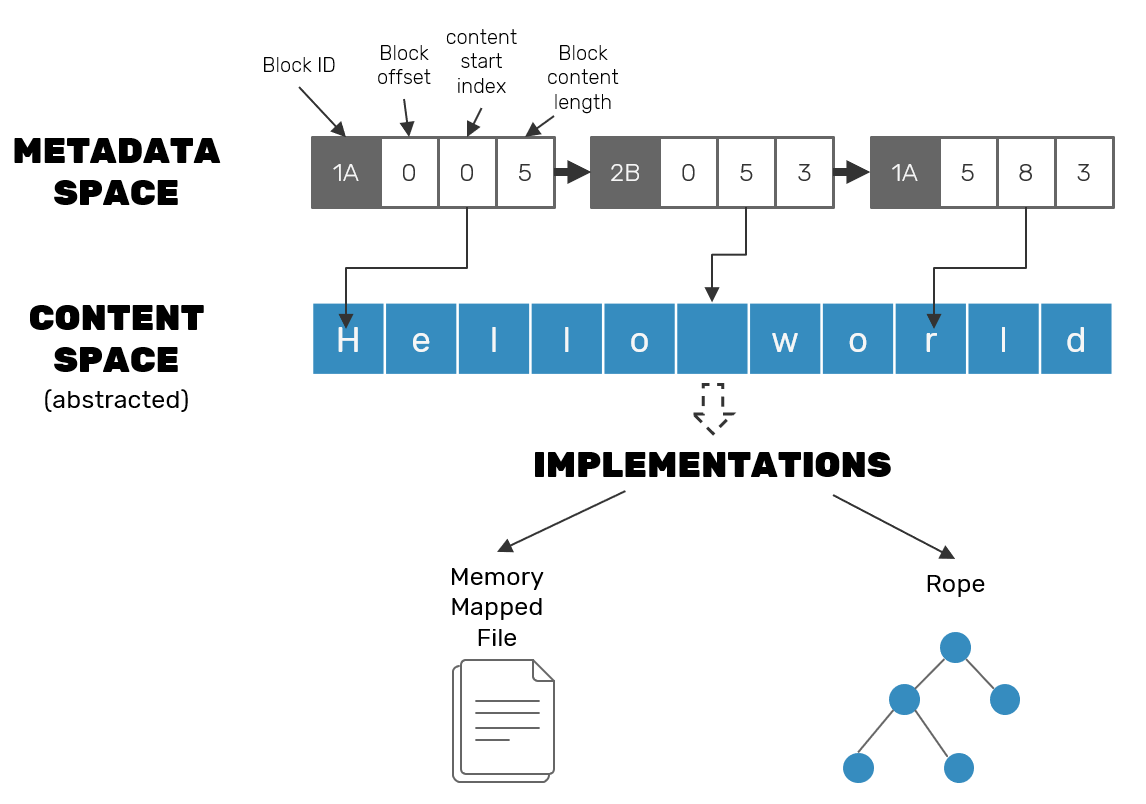
split-wise-rga-abstraction-1

On the other hand if we're about to make our content space aware of CRDT metadata, we could do optimizations like zero-copy split operations - splitting the block to insert a new one inside of it can be done solely on metadata nodes by shifting the indexes they point to, without any changes in the underlying string buffer. While this makes writes faster (they can be append-only) it comes at the price of making random-access on reads: we need to use block metadata info in order to know which parts of content store need to be read in what order.

The same idea can also work for deletions. In such case we first do a logical deletion, while a separate vacuum process can deal with physical removal and reordering of string fragments that are no longer in use.

More efficient delta-state propagation

In the past, we covered the case of state-based CRDTs. We also talked about the issue with passing a huge state objects between the peers to provide necessary eventual consistency, and how to mitigate these issues with deltas. Now, let's talk about what deltas do and don't solve.

We didn't really mentioned the guarantees of a replication protocol in case of deltas, as it wasn't really that necessary. We only mentioned that in the case when the delta-state is lost, we can make a full CRDT synchronization from time to time. What if that's not possible? What if our "full" state is a multi-terabyte collection of data?

Let's approach this issue using our delta-state OR-Set as an example. When we developed it in the past, we constructed it from 2 parts:

  1. A dotted vector version that described a "current time" as observed by our collection. This logical clock contained a compressed information about all dots (used to uniquely tag a single set insert operation) captured by the set.
  2. A map of (value, dots) where dots where unique IDs of insert operations (the same element could be inserted multiple times) that caused a value to appear in the set.

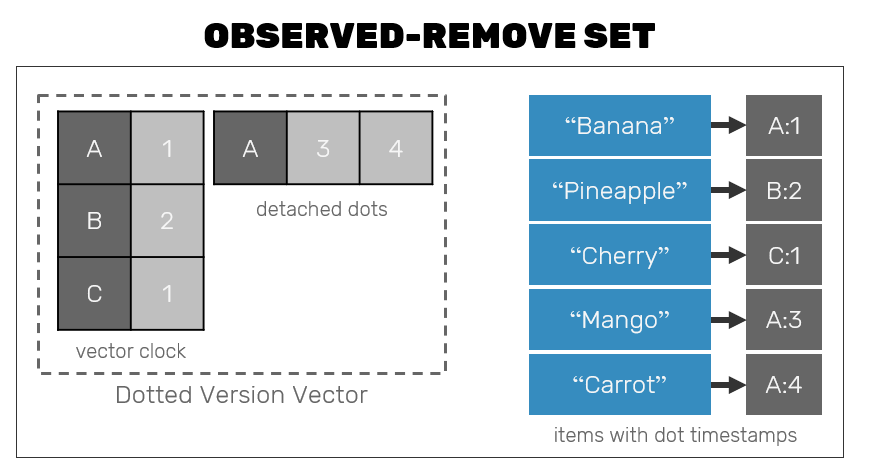
or-set

In our implementation we generated new dots only for inserts - we were able to do conflict resolution based on a fact, that if insert dot was present in dotted vector version (1) but not in a result map (2), then it must mean that this value was removed. This however is not a strict rule. We can generate dots for removals as well - in the past approach it was just wasteful, however now we're be able to utilize that extra information to decide if state of our set had changed based on the state of dotted vector version alone! But why? Since dotted version vector has compressed representation and its size is not dependent on the size of the elements stored in OR-Set, we can pass delta of version vector alone instead to signal to other replicas that our local state has changed!

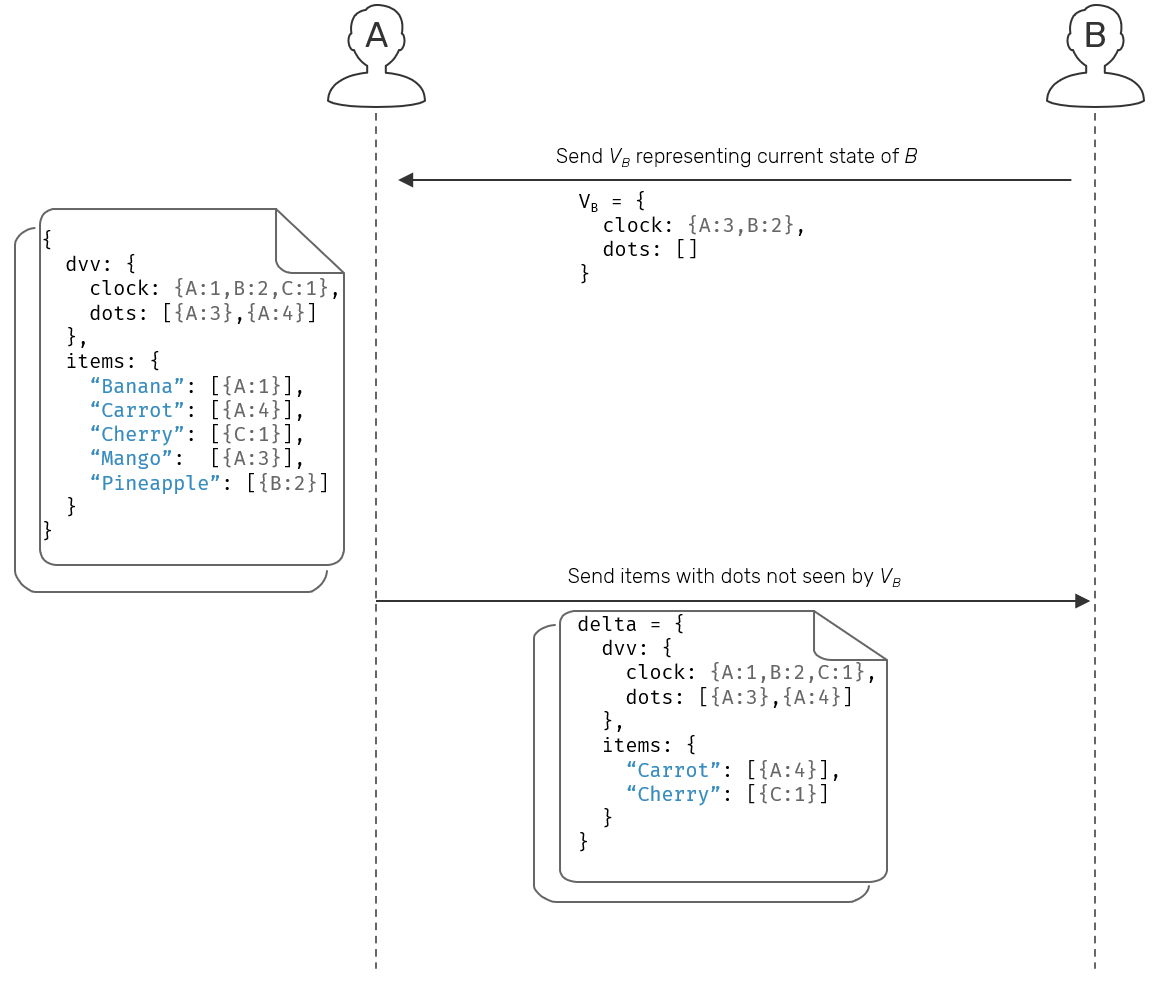
dvv-replication

Now, instead of one step replication, we can change it into request-response pattern. When looking for or notifying about updates, our replica is first going to pass a dotted version vector. Since it's usually smaller that the actual state of the set, the cost of that request is fairly low.

Another side can use this information to produce a diff between its own local version and incoming one, and use it to compute the delta-state that's exactly matching missing updates on the other side. This is possible, because version vectors contain identifiers of all update operations, while items are tagged with dots themselves. If we have the diff between local/remote DVV, all we need now is to gather all elements with dots found in that diff.

What's more interesting, we can go even further. We don't need to pass the versions all the time. All we really need to start the procedure is a simple digest (consistent hash) of the version vector itself.

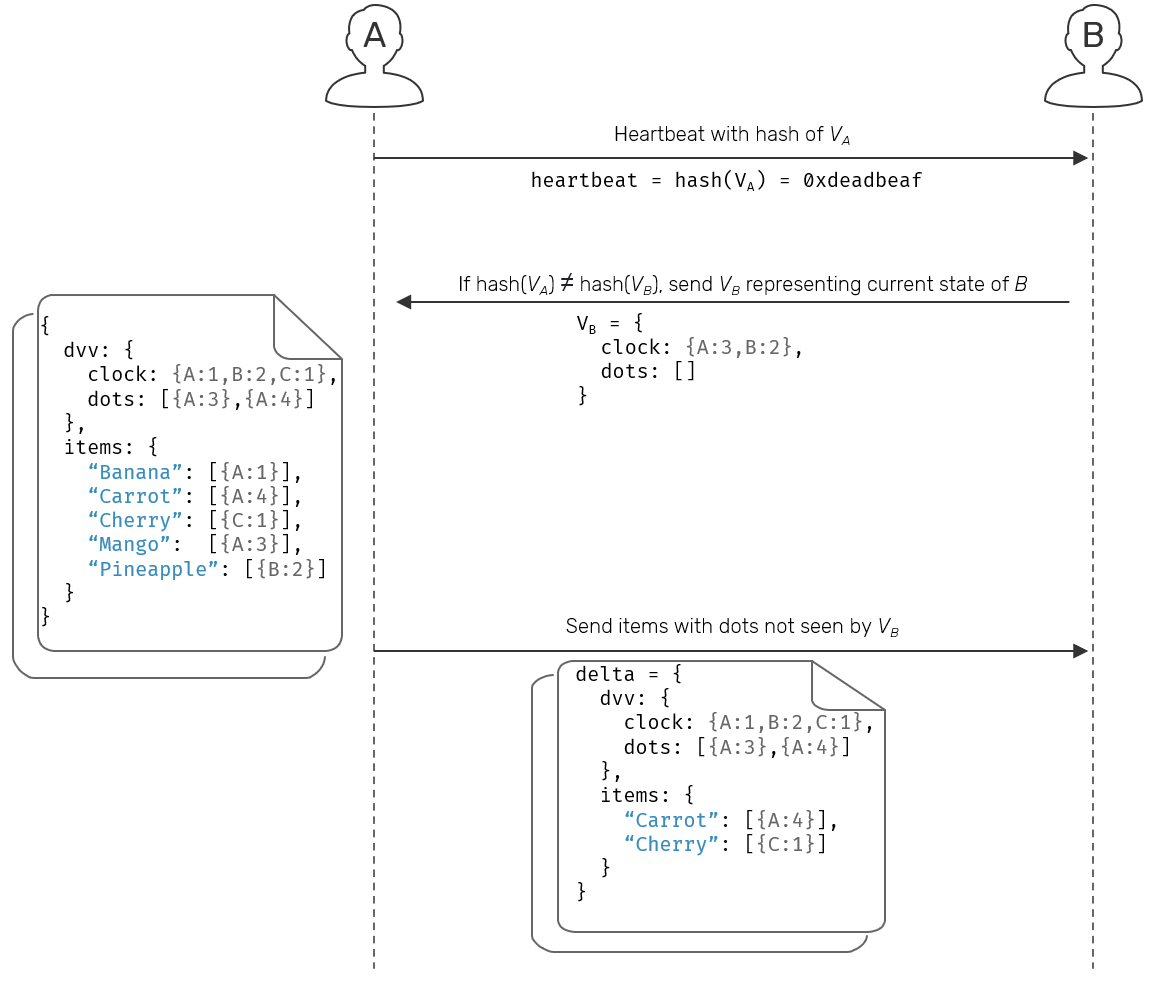
dvv-replication-digest

While this adds an extra network call to our replication process, the initial payload is so small that it could be as well piggybacked on top of i.e. heartbeat messages used to identify alive and dead nodes, which makes easier to determine when other peers have new data to share.

Associativity of events in operation-based CRDTs

Here we'll cover some ideas on how to optimize operation-based CRDTs. As we mentioned in the past, the core principle of op-based CRDTs is commutativity - since total ordering is not possible to maintain in system with multiple disconnected writers, we need this property to ensure that partially ordered events can be applied in different order.

While the associativity property was not required in operation-based variant (only in state-based one), we could also find improvements by applying this property to our events.

Associativity in this context means that we can conflate our events and apply their conflated representation to produce the same results, as if we'd apply them one by one. The obvious case for this is eg. counter incrementing. If we're not constrained with showing intermediate results - like when we use counters as sequencers, which I strongly discourage you to use CRDTs for anyway - we can assume that series of operations like [Inserted('A'), Inserted('B'), Inserted('C')] emitted in a row could be as well represented as a single [Inserted('ABC')].

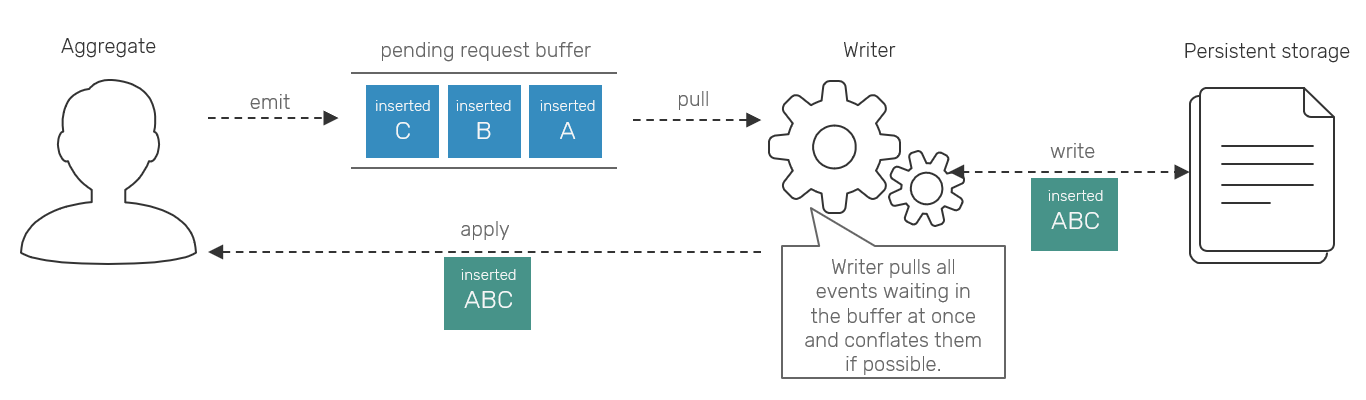
event-conflation

The optimization here comes from the fact, that under Reliable Causal Broadcast, each separate event requires a bunch of metadata and persistence prior to replication/applying. Quite common technique of working with requests incoming at higher rate than they're stored with is to buffer them and perform any necessary I/O operations on buffered chunks of data rather than small pieces alone.

We apply a very similar principle here, but at application logic level. Since the upstream and downstream can work at different rates, we replaced our event buffering with conflation: if upstream is producing events at the higher rate, they are conflated together into single one and emitted when downstream is ready. This approach plays well together with workflow oriented approach and backpressure mechanisms.

Keep in mind that while in context of CRDTs this is usually an applicable solution it may not work in more general business contexts. Oftentimes we want to distinguish events from each other on the logical level eg. bank transfer transactions. This sort of associativity may cause loss of business context information, so as always terms and conditions apply.

Indexing vector clocks

One of the issues with vector clocks is that they are not supported very well by present day data stores. Even while some of databases are using them internally, they are rarely exposed to developers and it's even less common that they have first class support for operations like indexing.

Some databases (like Postgres) have defined great extensibility points for the programmers to inject their own custom logic into DB runtime. One of the experiments, I'm working on is to add indexable vector clock support in PostgreSQL. If this succeeds, it will probably deserve it's own blog post, but here let's try to answer the question: since vector clocks don't comply to standard ordering rules (because they can be only partially ordered), can we even build indexes on top of them?

A powerhouse behind Postgres GiST indexes

Generalized search trees (GiST) are one of the index types available in PostgreSQL. Their capabilities are implemented in many native PG types like timestamp ranges, spatial data or full text searching. Here we won't go really deep inside of how they work. If you're interested and want to read more, I think this blog post is great for start.

The basic principle we are interested in is that Postgres let's us to define our own GiST compatible data type utilizing R-tree indexes. The idea behind them is that we split an N-dimensional space objects into smaller slices. Then we recursively split them further into even smaller blocks, until all indexed values contained within a given block will fit into a single database page. Out of all of these elements we build a multi-level tree with with higher levels (containing bigger pieces) descending into lower levels with smaller pieces.

While spatial indexes are the most visual representation of such approach, it is really generalizable into any N-dimensional space. And how can we represent coordinates in N-dimensional space? Using vectors!

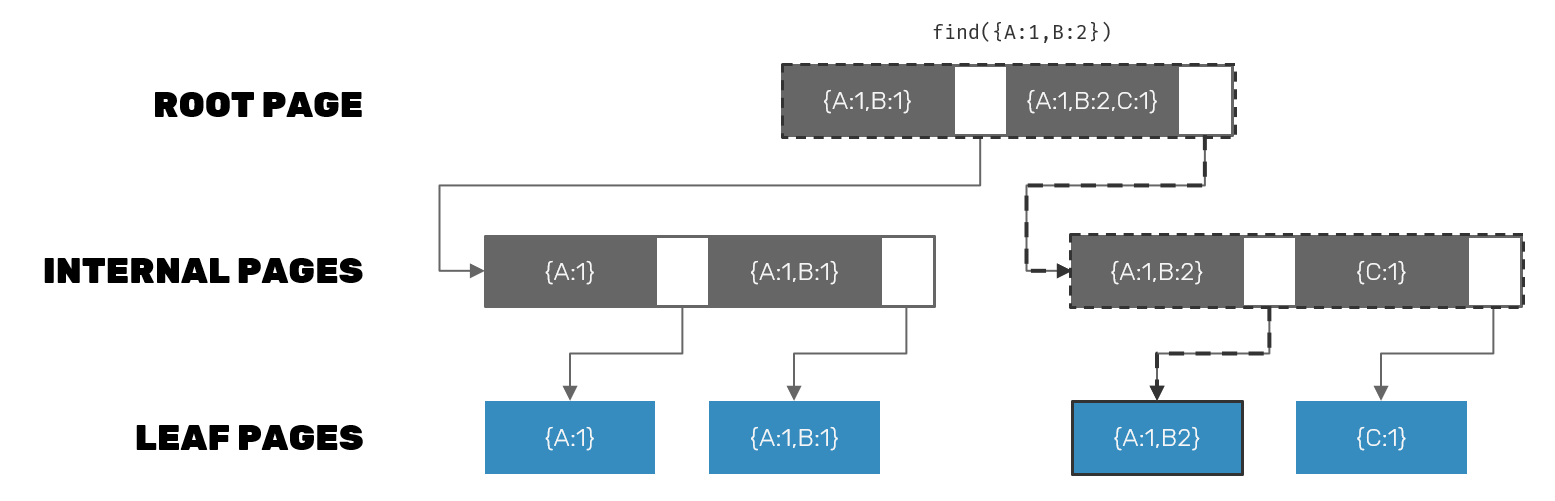
b-tree-index-1

We can translate vector clock partial comparison states into operators supported by Postgres:

  • If t1 is less than t2 we can say t1 is contained by t2 → t1 <@ t2.
  • If t1 is equal to t2, we say they are the same → t1 ~= t2
  • Greater case is analogous to less, so t1 contains t2 → t1 @> t2.
  • Finally, we can say that two concurrent vectors are concurrent when they overlap → t1 && t2

Additionally building GiST index requires defining some functions to be integrated into Postgres internals (you need a language that offers foreign function interface with C for that):

  • union which composes higher-level key out of lower level ones. We can implement it simply in terms of merging vector clocks.
  • equal to check if keys are equal. We already have that as part of partial comparison.
  • consistent to check if given index key satisfied the query/operator: in this case partial comparison operators we defined above.
  • penalty used to determine where it's least expensive to insert a new vector clock, given several possible pages that could fit this role.
  • picksplit used when given index page is getting too big - in that case we need to split it in two and determine which vectors are about to go into which page.
  • compress/decompress functions which allow us to use different data type to be used to represent index key - this may be useful to preserve space. For example: {A:2,B:1} may be good notion for a single vector clock but for many of them keeping IDs (A, B) is redundant. Instead we could have one global mapping for ID→index ([A,B] which tell us which replicas are mapped to which indexes), and represent each vector clock as an array with sequence numbers maching indexes of global mapping (eg. [2,1]), resulting in less disk space consumption.

The major challenge here is picksplit function implementation, as same-level vector placement will directly affect ability to narrow search space of an index. Fortunately many algorithms have been implemented for efficient space partitioning of R-Trees and some of them should be generalizable for vector clocks as well.

Faster vector clock comparison

The last optimization, I wanted to mention, is related to comparison operations over vector clocks. In many libraries vector clocks are implemented using maps. While this seems natural, it also comes with a cost - maps are not the most optimal things when it comes to efficient iteration over their elements, and this is exactly what we do when we want to compare them.

There's also other observation that we can take for our advantage - once a membership of our distributed system stabilizes, peer identifiers of our vector clocks stay the same, so do positions of their sequence numbers. We can optimize for that case by introducing SIMD operations.

The idea is simple - we keep our peer ids in one array, and their corresponding sequence numbers in another one. During comparison (but also potentially merging) we first check if peers of two vectors are equal - which in stable clusters should happen >99% of the time. If they are, it means that arrays with sequence numbers of both clocks have their elements under the same indexes. This means it's safe to load them into SIMD registers right away (given sequence number of 64-bits, a 512-bit SIMD instruction set can operate on 8 of them at once) and perform multiple comparisons / merges at once. Initial peer id check can also be done using SIMD registers.

How much faster is it? In example implementation, I've got 2 orders of magnitude speedup when compared to standard AVL-tree based implementation of vector clock. For smaller vector clocks it's less impressive (SIMD registers kick in for registers over certain size, but that can also be improved), but it's still faster, mostly because arrays are more hardware-friendly data structures than trees.

List of open source CRDT projects

There are many more optimizations in micro- and macro-scale, that are scattered throughout different projects. Let's make a few honorable mentions, where you can dive into to expand your knowledge further:

  • RiakDB (Erlang) which is probably the most well known open-source key-value database implementing delta-state CRDTs.
  • AntidoteDB (Erlang) which is an operation-based key-value database. One of its unique traits is support for interactive transactions - hopefully we'll cover an algorithm behind them in the future.
  • Lasp (Erlang) which implements many of operation-based and delta-state based CRDTs.
  • Y.js (JavaScript) which is an entire ecosystem - also one of the oldest and fastest in this domain - focused on adding collaborative support into rich text editors and applications. It uses delta-state CRDTs.
  • Automerge (JavaScript) which is another library in the domain of collaborative apps. It represents an operations-based approach to CRDTs.
  • Akka DistributedData (Scala and C#) which is a delta-state key-value store build on top of Akka framework.
  • Akka Replicated Eventsourcing (Scala) which is another library from Akka ecosystem, that seems to originate from ideas of Eventuate and offers an ability to create operation-based CRDTs on top of evensourcing paradigm - very similar to what we talked about before.
  • Pijul (Rust) which is a version control system (just like Git), that uses CRDT concepts to perform conflict resolution of commits (called patches in Pijul) submitted by different repository contributors.

While there are many many more, I decided to focus on the projects, that were released with open source and decent level of completeness.

Summary

We've mentioned some of the optimization techniques, that can be used to make our CRDTs better in real life workloads - some of these are already used in systems like ditto.live or y.js. Others have not yet been implemented at the moment of writing this post. While I'm going to post more about about conflict-free replicated data types in the future, I won't attach them to the common table of contents - I think this post serves as a good conclusion. If you're interested, keep an eye on #crdt tag on this blog.