In this post, we'll continue onto topic of Commutative Replicated Data Types. We already mentioned how to prepare first, the most basic types of collections: sets. This time we'll go take a look at indexed sequences with add/remove operations.

Other blog posts from this series:

Now, why I said that indexed sequences are more complex than sets? It doesn't reflect our intuition about ordinary data types, where usually set implementations are more complex than eg. arrays. Here it's all about guarantees: unlike sets, indexed sequences come with a promise of maintaining order of inserted items, which is much harder to maintain when we take into account that multiple actors may choose to insert/remove elements in such collection in disjoined, concurrent fashion.

Maintaining order is very useful in many places - like building queues/stacks being one of the more obvious - however there's one domain, which brags especially loud about it. That is text operations & collaborative text editors.

We're talking about fully decentralized collaboration, without any need of collaborators being online in order to perform updates or having a centralized server to resolve conflicting updates (see: Google Docs).

This area has been researched heavily over many years - many of the data structures created there predates term Conflict-free Replicated Data Types by years. Here we'll only mention two:

  • LSeq - Linear Sequences
  • RGA - Replicated Growable Arrays

PS: there's another (older and perhaps even more popular) approach to text collaboration popularized by Google Docs, Etherpad, xi etc. called operational transformation. Nowadays it's often a preferred choice because of maturity and a speed of its implementations. But the times are changing...

Problem description

Our scenarios here will work in context of inserting/deleting characters from some kind of text document, as this way seems to be the most well recognized and easy to visualize.

A key observation of most (if not all) CRDT approaches to ordered sequences is simple: we need to be able to track the individual elements as other elements in collection come and go. For this reason we mark them with unique identifiers, which - unlike traditional array index, which can refer to different elements over time - will always stick to the same element. While in literature they don't have a single name, here I'll call them virtual pointers.

LSeq

In case of LSeq these indentifiers are represented as sequences of bytes, which can be ordered in lexical order .eg:

// example of lexically ordered sequence
a   => v1
ab  => v2
abc => v3
b   => v4
ba  => v5

Since no generator will ever guarantee that byte sequences produced on disconnected machines are unique 100% of the time, the good idea is to make virtual pointer a composite key of byte sequence together with unique replica identifier (using replica ID to guarantee uniqueness is quite common approach). Such structure could look like this:

[<Struct;CustomComparison;CustomEquality>]
type VPtr =
  { Sequence: byte[]; Id: ReplicaId }
  override this.ToString() =
    String.Join('.', this.Sequence) + ":" + string this.Id 
  member this.CompareTo(other) =
    let len = min this.Sequence.Length other.Sequence.Length
    let mutable i = 0
    let mutable cmp = 0
    while cmp = 0 && i < len do
      cmp <- this.Sequence.[i].CompareTo other.Sequence.[i]
      i <- i + 1
    if cmp = 0 then
      // one of the sequences is subsequence of another one, compare their 
      // lengths (cause maybe they're the same) then compare replica ids
      cmp <- this.Sequence.Length - other.Sequence.Length
      if cmp = 0 then this.Id.CompareTo other.Id else cmp
    else cmp

In order to insert an element at given index, in LSeq we first need to find virtual pointers of elements in adjacent indexes, then generate new pointer, which is lexically higher than its predecessor and lower than its successor (lo.ptr < inserted.ptr < hi.ptr).

There are many possible ways to implement such generator - the trivial one we're going to use is to simply compare both bounds byte by byte and insert the byte that's 1 higher than a corresponding byte of the lower bound, BUT only if it's smaller than corresponding byte of the higher bound:

let private generateSeq (lo: byte[]) (hi: byte[]) =
  let rec loop (acc: ResizeArray<byte>) i (lo: byte[]) (hi: byte[])  =
    let min = if i >= lo.Length then 0uy else lo.[i]
    let max = if i >= hi.Length then 255uy else hi.[i]
    if min + 1uy < max then
      acc.Add (min + 1uy)
      acc.ToArray()
    else
      acc.Add min
      loop acc (i+1) lo hi
  loop (ResizeArray (min lo.Length hi.Length)) 0 lo hi

If virtual pointers on both bounds are of different length we can replace missing byte by 0 and 255 respectivelly. If there's no space to put a free byte between both bounds, we simply extend the key by one byte, eg. we need to generate key between [1] and [2] → the resulting key will be [1,1].

These boundary keys must only exists at the moment of creating a new event (so in prepare/command-handler phase), but are not necessary when we're about to apply it. This makes element deletion an incredibly simple procedure - all we need to do, is to just remove a corresponding entry from our collection.

let private crdt (replicaId: ReplicaId) : Crdt<LSeq<'a>, 'a[], Command<'a>, Operation<'a>> =
  { new Crdt<_,_,_,_> with
    member _.Effect(lseq, e) =
      match e.Data with
      | Inserted(ptr, value) ->
        let idx = binarySearch ptr lseq
        Array.insert idx (ptr, value) lseq
      | Removed(ptr) -> 
        let idx = binarySearch ptr lseq
        Array.removeAt idx lseq
    // other methods...
  }

If you're interested to see it in details, the code we described in this section can be found here.

Interleaving

Every CRDT comes with its tradeoffs, and LSeq is no different. One issue of LSeq data type is how it deals with concurrent updates. Imagine following scenario:

Two people, Alice and Bob, want to collaborate over a text document. Initial document content was "hi !". While offline, Alice edited it to "hi mom!", while Bob to "hi dad!". Once they got online, their changes were synchronized. What's an acceptable state of the document after sync?

While original LSeq insertion algorithm didn't specify insertion of multiple elements we can replace it with series of single character inserts.

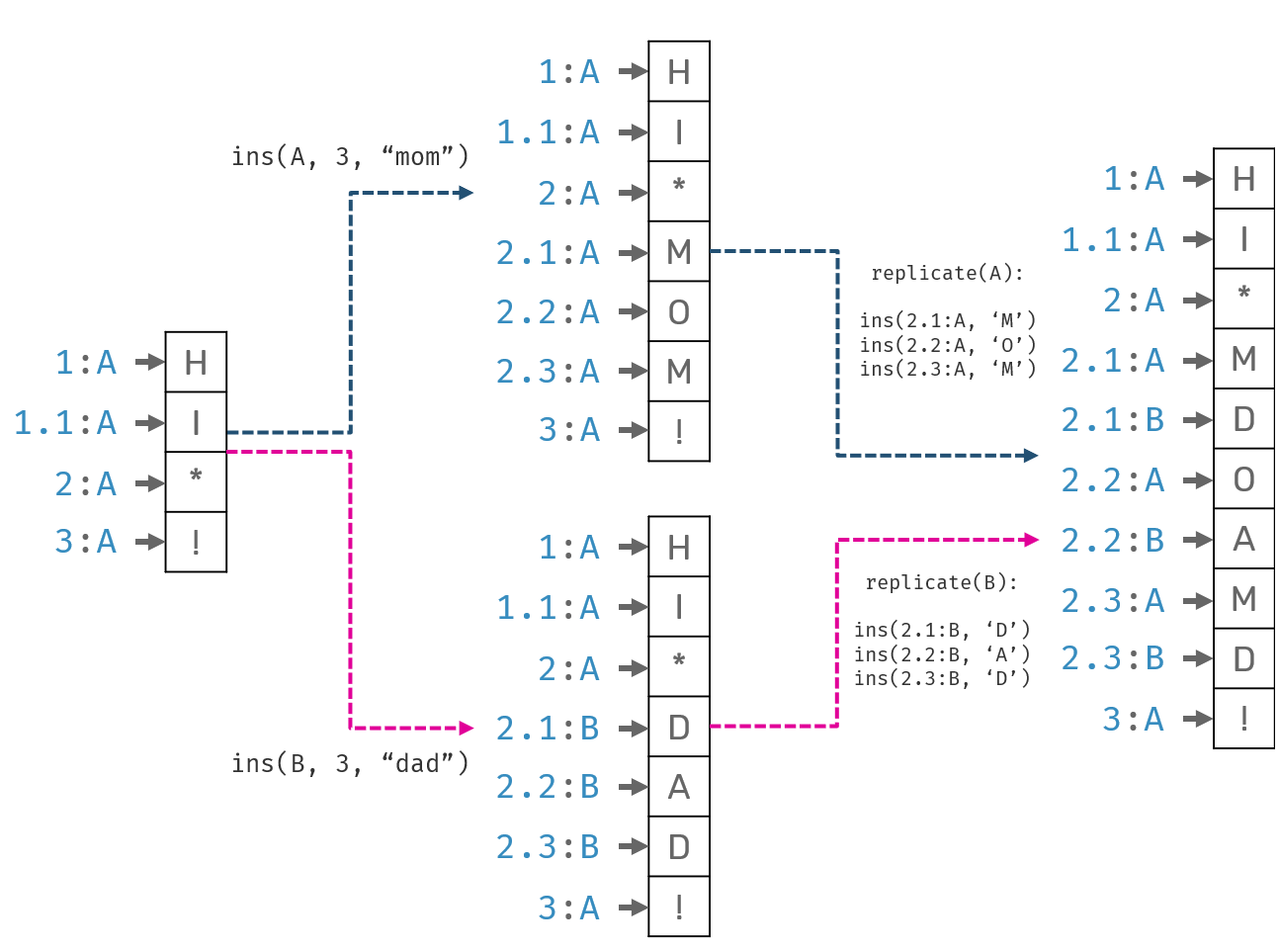
lseq-interleaving-4

Now, as you see here, after replication document on both sides contains "hi mdoamd!". While technically correct, it's doubtfully a desired outcome: we may guess that mixed output would satisfy neither Alice nor Bob's expectations. We missed the intent: a correlation between inserted elements. This problem can be solved (or at least amortized) in theory: we just need to generate byte sequences in a "smart way", so that elements pushed by the same actor one after another will land next to each other after sync. Problem? So far no one presented such "smart" algorithm.

PS: Based on the byte sequence generation algorithm you may even trace the order in which particular characters where inserted using only virtual pointers.

RGA

A second data structure we're going to cover now is known as Replicated Growable Array (RGA for short). I'll be refering to code, which full snippet you can find here. It ofers slightly different approach: where LSeq virtual pointers where byte sequences, in RGA it's just a combination of a single monotonically increasing number and replica identifier:

type VPtr = uint64 * ReplicaId

Now, we'll use this structure to (permanently) tag our elements. These together will form a vertex:

type Vertex<'a> = VPtr * 'a option

As you may see, here is the catch - our element is of option type. Why? In case of LSeq, virtual pointers where generated to reflect a global lexical order that matches the insertion order. They were not related ot each other in any other way. In case of RGA, pointers are smaller and of fixed size, but they're not enough to describe insertion order alone. Instead insert event refers to a preceding virtual pointer. For this reason we cannot simply remove them, since we don't known if another user is using them as reference point for their own inserts at the moment. Instead of deleting permanently, RGA puts tombstones in place of removed elements.

type Command<'a> =
  | Insert of index:int * value:'a
  | RemoveAt of index:int
        
type Operation<'a> =
  | Inserted of predecessor:VPtr * ptr:VPtr * value:'a
  | Removed of ptr:Position

Advantage here is that - because RGA insert relates to previous element - the sequences of our own inserts will be linked together, preventing from interleaving with someone else's inserts.

Simple question: how are we going to put first element, since there are no predecessors? When initiating an empty RGA, we can put an invisible header at its head as a starting point:

let private crdt (replicaId: ReplicaId) : Crdt<Rga<'a>, 'a[], Command<'a>, Operation<'a>> =
  { new Crdt<_,_,_,_> with
      member _.Default = 
        let head = ((0,""), None)
        { Sequencer = (0,replicaId); Vertices = [| head |] }
    // other methods...
  }

PS: in this implementation, we're using an ordinary array of vertices, but in practice it's possible to split metadata and contents into two different structures and/or use specialized tree-based data structures (like ropes) to make insert/remove operations more efficient.

Now, how the insertion itself should look like? First we need to find an actual index, where a predecessor of inserted element can be found. Then just insert our element under next index. This sounds simple, but it misses one crucial edge case: what if two actors will concurrently insert different elements after the same predecessor?. The resulting collection after replication should present all elements in the exact same order. How could we achieve this?

Again we'll use our virtual pointers, and extend them with one important property - we'll make them ordered (first by sequence number, then replica ID), just like in the case of LSeq. Now the rule is: recursivelly, we shift our insertion index by one to the right every time when virtual pointer of the element living under that index already had a higher value than virtual pointer of inserted element.

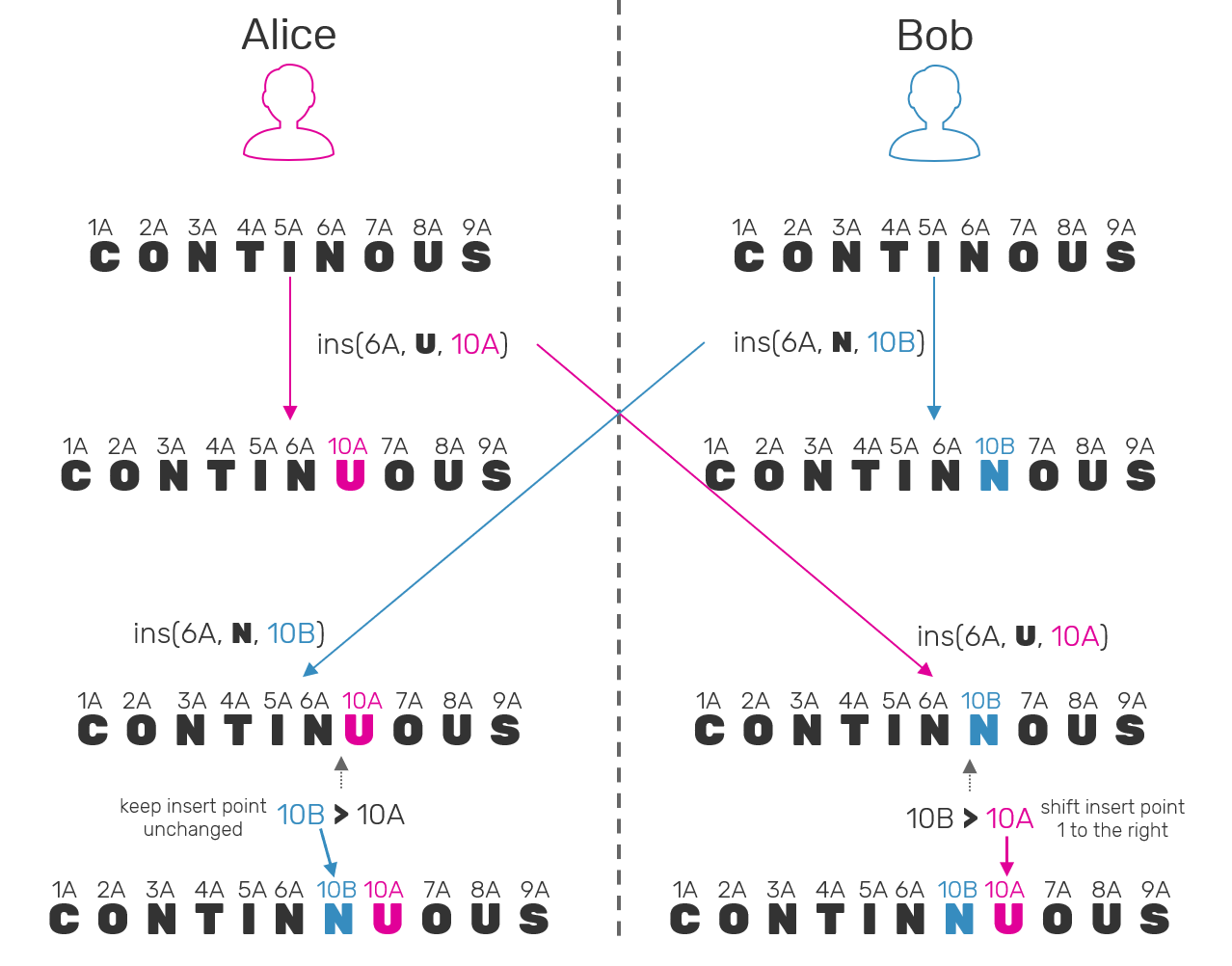
rga-insert-shift

Why does it even has any sense? Well, remember when generating new virtual pointer, we take a sequence number as the highest possible value? Also since our RGA is operation-based, we can count on the events being applied in partial order. Using example: when inserting element C after A inside of collection [A,B], we can be sure that B has virtual pointer that falls into one of two categories:

  1. Bs pointer has sequence number lesser than C's which means, we can be sure that B was inserted before C, not concurrently. So the user must have knew about existence of B and still decided to insert C after A.
  2. B pointer's sequence number is equal or greater than Cs - that means that B has been inserted concurrently on another replica. In this case we also compare replica ID to ensure that virtual pointers can be either lesser or greater to each other (but never equal). This way even when having partially ordered log of events we can still guarantee, that elements inside of RGA itself will maintain a total order - the same order of elements on every replica.

Another indirect advantage of having CRDT backed by a log of events is that we can travel over entire history of edited document and see its state at any point in time!

This check is performed recursively, and can be written as follows:

let rec private shift offset ptr (vertices: Vertex<'a>[]) =
  if offset >= vertices.Length then offset // append at the end
  else
    let (successor, _) = vertices.[offset]
    // F# creates structural comparison for tuples automatically
    if successor < ptr then offset
    else shift (offset+1) ptr vertices // move insertion point to the right

With this we can implement our insert operation as:

let private applyInserted (predecessor: VPtr) (ptr: VPtr) value rga =
  // find index where predecessor vertex can be found
  let predecessorIdx = indexOfVPtr predecessor rga.Vertices
  // adjust index where new vertex is to be inserted
  let insertIdx = shift (predecessorIdx+1) ptr rga.Vertices
  let newVertices = Array.insert insertIdx (ptr, Some value) rga.Vertices
  // update RGA to store the highest observed sequence number 
  // (a.k.a. Lamport timestamp)
  let (seqNr, replicaId) = rga.Sequencer
  let nextSeqNr = (max (fst ptr) seqNr, replicaId)
  { Sequencer = nextSeqNr; Vertices = newVertices }

With inserts done, the hard part is now over. We can get to removing elements at provided index (which we already described above). It's extremelly simple in comparison:

let private applyRemoved ptr rga =
  // find index where removed vertex can be found and tombstone it
  let index = indexOfVPtr ptr rga.Vertices
  let (at, _) = rga.Vertices.[index]
  { rga with Vertices = Array.replace index (at, None) rga.Vertices }

All we really need, is to mark a particular vertex as tombstone (here done by clearing its content to None) and skip them over when materializing our CRDT to a user-facing data structure:

let private crdt replicaId : Crdt<Rga<'a>, 'a[], Command<'a>, Operation<'a>> =
  { new Crdt<_,_,_,_> with
      member _.Query rga = rga.Vertices |> Array.choose snd // skip empty vertices
      // other methods ...
  }

What's next?

We only scratched the surface here. The number of possible extra operations and optimizations that have been found here is trully astounding. We (probably) won't cover all but few of them on this blog.

  1. As we mentioned earlier, in RGA approach we don't physically delete removed vertices. Instead we tombstone them. That could be wasteful in case of frequently used, delete heavy, long living collections. However pruning of tombstones is actually possible. We'll cover that up another time.
  2. For specific cases like text editors, we'd like to insert entire range of elements (eg. characters) at once. This implementation doesn't allow us to do so. Imagine copy/pasting entire page of text, which would result in producing possibly thousand instantaneous insert operations. Again, it's possible to modify that implementation to make it work (it's called string-wise or block-wise RGA) and it's also in the plans for the future blog posts.
  3. RGA implementation adds a small metadata overhead to every inserted element (needed because of virtual pointer references). For small elements (eg. again, single characters) this may result in metadata constituting a majority of the entire payload. I can recommend you a presentation made by Martin Kleppmann about how this has been solved by using a custom formatting in the Automerge - a JavaScript library that allows us to use JSON-like datastructures with CRDT semantics. PS: another known library in this space is Y.js, which also uses optimizations in that area.